Can LLMs solve novel tasks? Induction heads, composition, and out-of-distribution generalization
This post is based on my recent paper published in PNAS. If you can’t get past the paywall, here is a arXiv version. Big thanks to my collaborator Jiajun Song and Zhuoyan Xu!
Can LLMs solve novelty tasks? The AGI debate
Since ChatGPT, there have been a lot of polarizing opinons about LLMs. One focal point is the novelty of the generated texts by an LLM.
Proponents point to the examples of creative solutions produced by ChatGPT and Claude, hailing these models as AGI or superhuman intelligence. Others argue that these models are simply parroting internet text and incapable of generating truly original generation.
Well…it all depends on how you define novelty and creativity, in my opinon. In statistics, a standard and well-studied situation is to train a model on data drawn from the training distribution \(P_{\mathrm{train}}\) and evaluate it on the same test distribution \(P_{\mathrm{test}}\). This classical notation of generalization requires training a model for each specific task. As many researchers know, GPT-3 and ChatGPT are smarter than that—which is epitomized by the in-context learning (ICL).
Here is a simple proposal to study “novelty” of models, which is often called out-of-distribution (OOD) generalization: \(\begin{aligned} P_{\mathrm{train}} \neq P_{\mathrm{test}}. \end{aligned}\)
LLMs generalize OOD on certain reasoning tasks
Let’s say someone asks you to play a game: given a prompt
“Then, Henry and Blake had a long argument. Afterwards Henry said to”
what is the next probable word? It is easy to guess Blake as the natural continuation. Now what if the prompt is changed a bit?
“Then, \&\^ and #$ had a long argument. Afterwards \&\^ said to”
It may take you some time to realize that I simply replaced the names with special symbols. Once seeing this point, you probably say #$.
Another example of symbolic replacement is a variant of ICL:
baseball is $#, celery is !\%, sheep is \&*, volleyball is $#, lettuce is
This prompt asks you to classifying objects into three classes, which are represented by…well…strange symbols. If you follow the replacement logic, then you will probably guess the natural continuation !\%.
While LLMs (especially earlier versions) are unlikely to have seen these strange artificially modified sentences during pretraining, we do see a point in these examples. Training data are mixed with natural languages, math expression, code, and other formatted text such as html. Testing models with perturbed prompts help us understand what models can do and cannot do.
A simple experiment shows how some of the open-source LLMs perform on these two tasks, with and without symbol replacement.
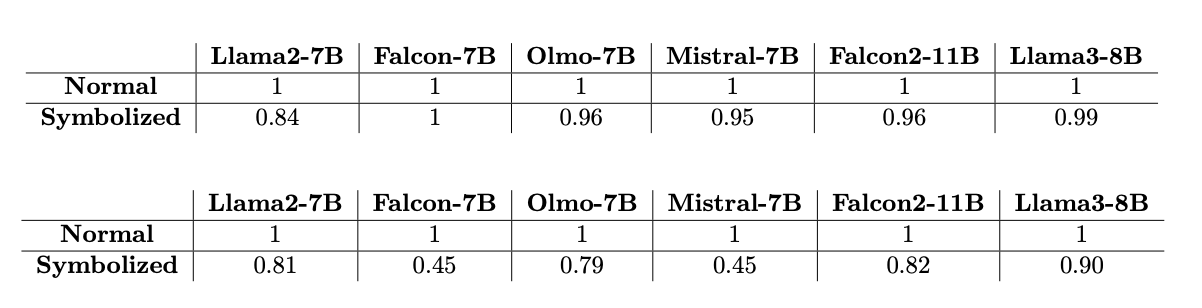
So, do LLMs solve novel tasks? I’d say yes, because the models seem to have figured out (not perfectly but definitely better than random guess) the “replacement rule” even when they are not explicitly trained on the above specific examples. Instances of the similar nature are observed in the literature, promoting the “Spark of AGI” argument.
Representation of concepts and linear representation hypothesis (LRH)
Can we undestand the model’s mechanism a bit better? In the past two years, a lot of interpretability analyses focus on the representation of concepts within a Transformer, most notably the sparse autoencoder (SAE) papers, one from Anthropic and another from OpenAI last year. These papers examine the embeddings (or hidden states) of a prompt, which is a simply a vector in the Euclidean space. My previous blog also explores the geometry of embeddings across network layers.
A key observation is the following:
Concepts are represented as linear subspaces in the embedding space.
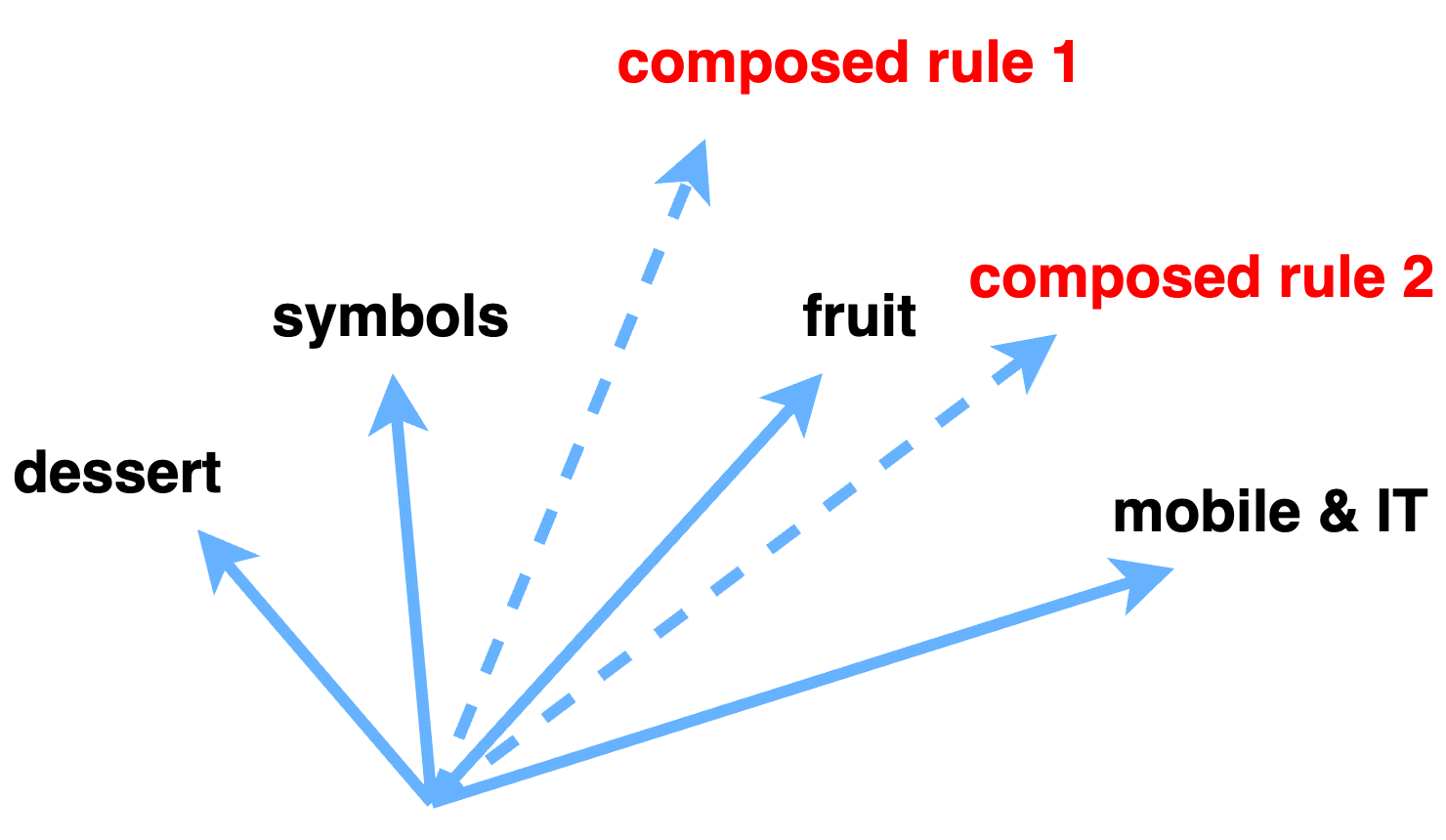
Let me give you a concrete example. Suppose that I have a prompt that contains the word “apple” as the last word. Now if I pass the prompt into an LLM, how does the embedding vector looks like?
Representing a word or a prompt as a linear combination of base concepts is an important intution for explaining the inner workings of LLMs. It is often referred to as the linear representation hypothesis (LRH).
\[\begin{aligned} \text{apple} = 0.09 \times \text{dessert} + 0.11 \times \text{organism} + 0.16 \times \text{fruit} + 0.22 \text{mobile\&IT} + 0.42 \times \text{other} \end{aligned}\]This decomposition captures possible scenarios where the word apple appears in a context: it sometimes mean a fruit, or a sweet dessert (apple pie!), or of course your favorite iphone. The remaining unexplained component may contain other contextualized information.
If you are familiar with word embedding, similar phenomenon is also observed there: “King” - “Queen” \(\approx\) “Man” - “Woman”. Broadly speaking, this can be viewed as a form of factor models in statistics.
How is composition represented inside a Transformer?
The LRH helps us to understand the representation of concepts in Transformers. But what about compositions? To find out how compositions are represented, let’s consider a simple copying task:
\[\begin{aligned} \ldots [A], [B], [C] \ldots [A], [B] \quad \xrightarrow{\text{next-token prediction}} \ldots [A], [B], [C]\ldots [A], [B],{[C]}. \end{aligned}\]Here \([A], [B], [C]\) are three words (or tokens) in a prompt where irrelevant words may sit between the patterns. The goal is for the model to copy the repetition pattern.
Tasks of similar nature have been studied in the induction head literature.
An induction head is an attention head in a Transformer with certain copying-related behavior.
Let me summarize a few interesting phnenomena about induction heads.
- Induction heads can be used to solve copying, which requires at least two self-attention layers.
- Once induction heads appear in a Transformer, they can generalize on OOD data.
- Induction heads are important to the emergence of ICL and accompany phase transitions in training dynamics.
In our experiment, we trained a two-layer Transformer on synthetic sequences that contain repetition patterns. We evaluated the model on two test data, one with the same distribution as the \(P_{\mathrm{train}}\)(in-distribution or ID) and another on a different distribution where we changed the token distribution and increased the pattern length (OOD). The following figure is what we got.
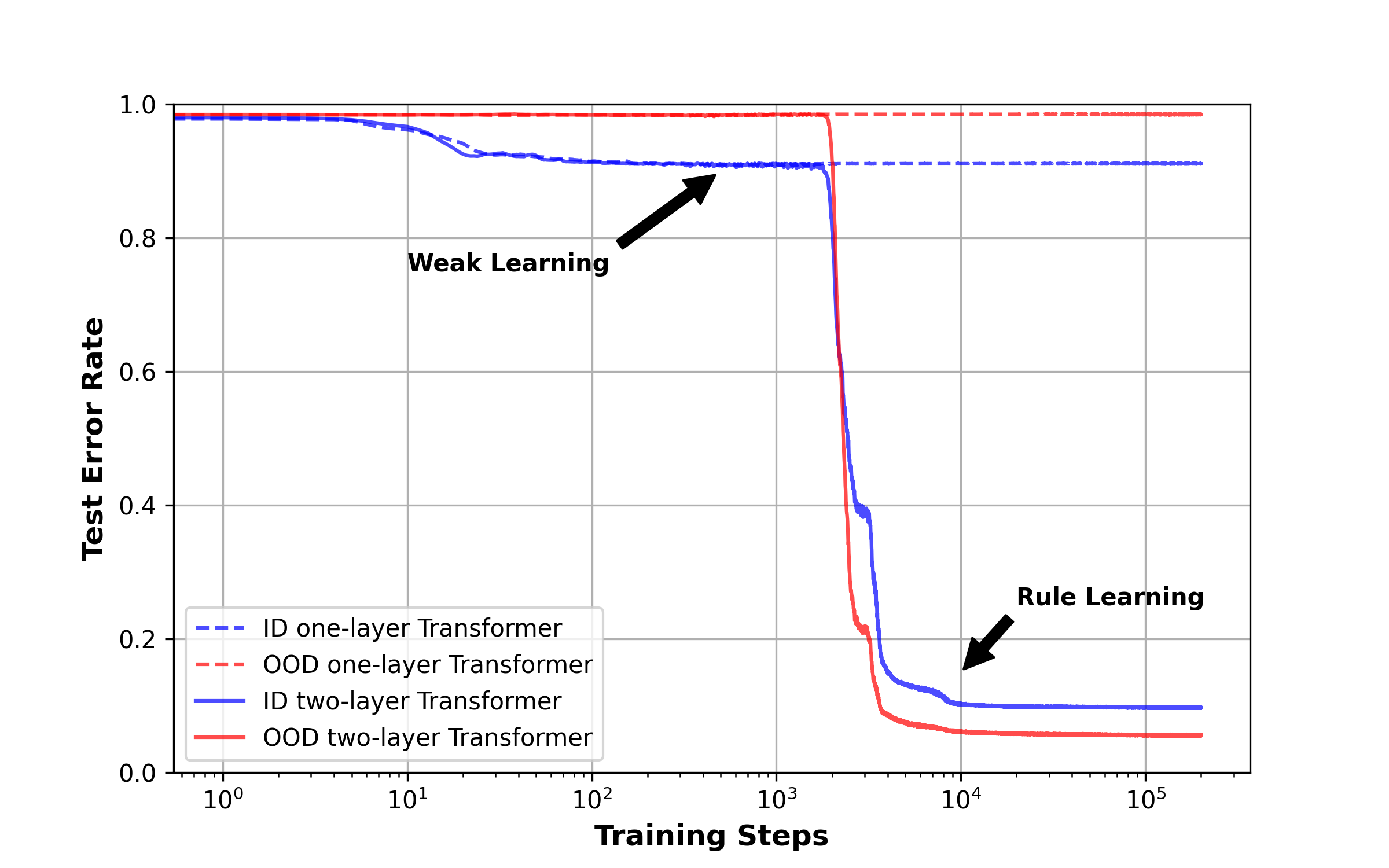
In the training dynamics, the model visibly experiences two phases.
- Weak learning: the model bases its prediction on the marginal distribution of tokens. It helps in-distribution accuracy a bit, but does not help and OOD accuracy.
- Rule learning: the model figures out the copying rule by forming the induction head, thus achieving low ID/OOD errors. We also found that two-layer Transformer, in comparison, did not learn how to solve copying.
Subspace matching
How do we explain this sudden emergence of induction heads and OOD generalization? (“Why does the model suddenly get smarter?”) We’ve taken many other measurements when training the Transformer. Roughly speaking, our findings can be described as follows.
The first self-attention layer outputs intermediate vectors in a subspace, and the second self-attention layer reads vectors from in another subspace. The two subspaces becomes suddenly aligned at the transition.
This provides an explanation for how compositional structures are formed within a model.
From LRH to Common Bridge Subspace Hypothesis
This simple experiment motivates us to generalize LRH to representation of compositions.
For compositional tasks, a latent subspace stores intermediate representations from the outputs of relevant attention heads and then matches later heads.
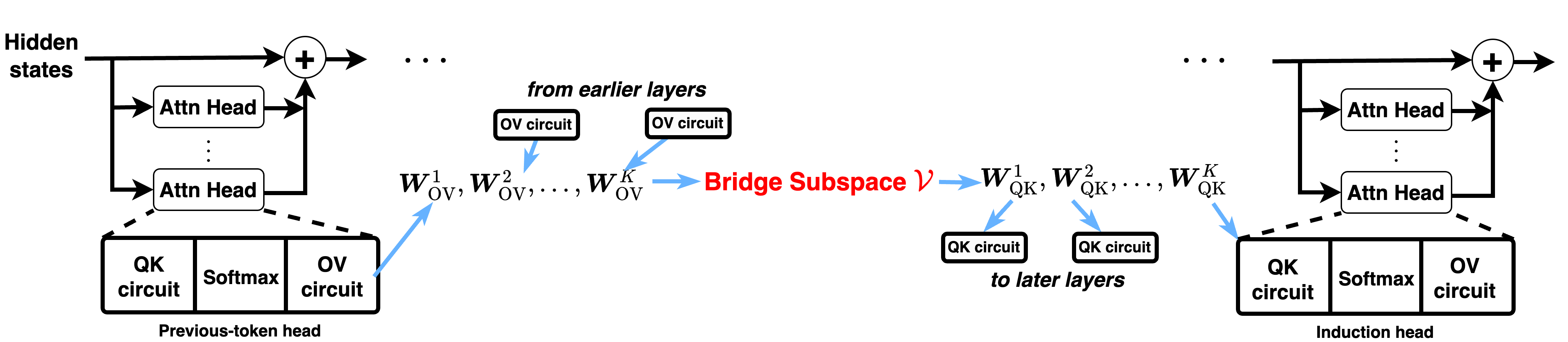
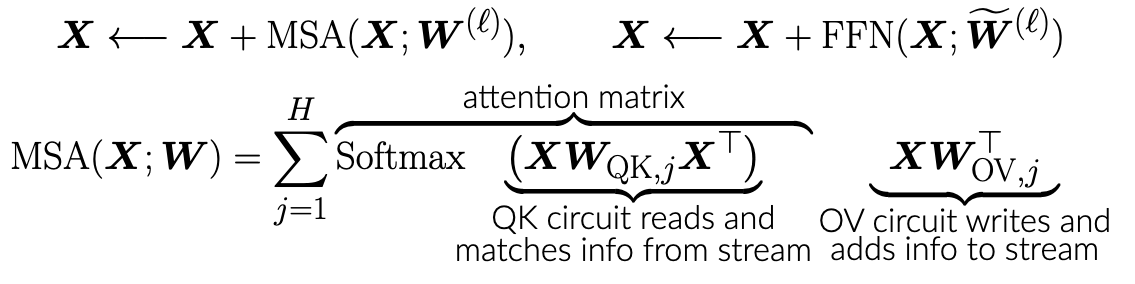
To be more clear, each self-attention layer has a weight matrix \(W_{\mathrm{OV}}\) responsible for “writing” the information, and a weight matrix \(W_{\mathrm{QK}}\) responsible for “reading” the information. This is in fact the intuition behind many mechanistic interpretability papers. If you are familiar with how Transformers work, then the following formula may help you understand the circuits perspective.
Mathematically, the common bridge subspace hypothesis can be stated as
\[\begin{equation} V = \mathrm{span}(W_{\mathrm{OV}}) = \mathrm{span}(W_{\mathrm{QK}}) \end{equation}\]for selected OV and QK weight matrices. The subspace \(V\) can be viewed a “bridge subspace” that connects two layers in order to represent compositions.
We’ve tested this hypothesis with projection-based ablation studies on many LLMs, and it appears to hold broadly. If you are thoughts on this hypothesis, dropping me a message is extremely welcome!
Induction heads are critical components across LLMs and tasks
A lot of our analyses center on induction heads, because they are so pervasive and important! They help us gain a lot of understanding about composition, OOD generalization, and geometric insights such as the common bridge subspace hypothesis.
We’ve confirmed prior findings about induction heads on a variety of LLMs (10+ models, ranging from 36M to 70B) on several tasks:
- Fuzzy copying
- Indirect object identification
- In-context learning
- Math reasoning with chain-of-thought on GSM8K
We’ve conducted ablation experiments where we removed induction heads from the model one by one and then measured the accuracy. Below are some representative plots.

So removal of induction heads leads to a significant drop of accuracy on symbolic prompts (recall the first figure), but not on the normal prompts. This result paints a likely picture about how LLMs solve language tasks.
LLMs rely on memorized facts for ID prompts, and use combined abilities (both memorized facts and IHs) to solve OOD prompts.
Final thoughts
Our study is far from complete, but I am excited that many interesting phenomena have emerged. It is worth thinking about a number of questions.
- Interpreting feature representations with better decomposition.
SAEs have been successful in explaining what models “believe” at a given layer. However, many questions remain unclear to me, such as
- how concepts are composed across layers,
- how models solve complicated reasoning tasks, and
- how the rules are represented by models Perhaps we can identify more structures that do not represent base concepts but are functionally important. The observation of bridge subspaces may be useful.
- Memorization and generalization. It is still not clear to me how models pick up and memorize concepts, and use some of the memorized concepts selectively in a context. Especially for reasoning models such as OpenAI’s o1 and DeepSeek-R1. It’s definitely more costly if I am going to run complicated reasoning experiments. Hopefully I can get some help this year :-)